---

In this lab you will write a program consisting of multiple functions that dabble in analytic geometry.

---

1. Teams

   You are encouraged to work with a partner for this lab. You and your partner should begin thinking about the problems and begin writing the code before lab time.

2. What to do

   Unlike earlier labs, I have provided most of the program for you below. The complete program consists of two files. Your task is to create a Python module consisting of four functions that my code will use.

   The program requests four floating-point numbers from the user. These four values, in order, represent the x₁, y₁, x₂, and y₂ components of the two geometric points (x₁, y₁) and (x₂, y₂).

   The program then does four things:

   1. Computes and displays the distance between the points.
   2. Computes and displays the slope of the line that passes through the two points.
   3. Computes and displays the y-intercept of the the line that passes through the two points. If the line is a vertical line, the program computes the x-intercept instead.
   4. Prints, in slope-intercept form, the equation of the line that passes through the two points.

   Each of the above four tasks is handled by separate functions as described below. Your task is to write those functions.

   • Distance

     The distance between two points (x₁, y₁) and (x₂, y₂), is given in the following formula:

     

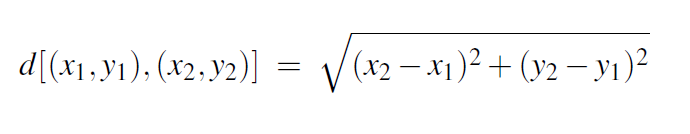
     Write a function named distance that accepts four floating-point arguments x₁, y₁, x₂, and y₂, in that order, representing two geometric points. It should return the floating-point value representing the distance between the two points.

   • Slope

     The slope of the line passing through two points (x₁, y₁) and (x₂, y₂), is the difference of the y values divided by the difference of the x values:

     

     Write a function named slope that accepts four floating-point arguments and returns the floating-point value representing the slope of the line passing through the two points represeted by the arguments.

     Watch out for vertical lines! Return the value None to represent infinity if the line is vertical.

     Note: The function's behavior is undefined for parameters that represent two equal points. When we say the function's behavior is undefined, we mean you do not need to worry about what your function does if the client attempts to compute the slope with two points that are the same.

   • Intercept

     An intercept is a number that represents a location on an axis where a line intersects that axis. The y-intercept of a line is the y value of the point where a line crosses the y-axis. Write a function named intercept that accepts four floating-point arguments representing the coordinates of two points. The function ordinarily returns the floating-point value representing the y-intercept of the line that that passes through the two points defined by the arguments.

     For non-vertical lines, we can compute the y-intercept from the y = mx + b form of a line. Solving for b, we get b = y - mx:

     

     This means if we know the slope, m, we can plug in the (x, y) coordinates from either point to compute b.

     Vertical lines do not have a y-intercept, so the intercept function instead should return the x-intercept for vertical lines. If the two points form a vertical line, it is easy to determine the x-intercept.

     Note: The function's behavior is undefined for parameters that represent two equal points. Again, this means you need not worry about this possibility in your function.

   • Line equation

     The equation of a line in slope-intercept form is

     y = mx + b where m is the line's slope, and b is the line's y intercept.

     Write a function named line_equation that accepts two floating-point arguments representing the slope and y-intercept of a line. It prints the the equation of that line in slope-intercept form. The function returns nothing.

     If the first parameter a caller passes to the function is None, the line is considered vertical. In this case the second parameter represents the x-intercept instead of a y-intercept. A vertical line has an equation of the form

     x = b

     where b is the x-intercept. Your function should print the equation for vertical lines correctly.

     If your line_equation function displays the correct mathematical results and the other three functions are correct, you will receive 9/10 points for this assignment. To receive the full 10/10 score, on the first or second test of your program on or before the due date the equation your function prints should be "pretty," meaning do not print an equation like

     y = -1x + -3
     rather the function should print
     y = -x - 3
     and an equation like
     y = 20.5x + 0
     should appear as
     y = 20.5x
     This means you will need some conditional statements within your line_equation function to fine tune the exact output. As you begin developing your line_equation function do not worry about pretty output. First concentrate on getting the numbers correct, and after you are sure the displayed results are mathematically sound then, if you have time, proceed to make the output more attractive.

3. Simple Test Code

   You can use the following Python program, geotest.py, as is. It performs a very rudimentary test of your code.

   # File geotest.py ################################################################ # You do not need to modify anything in this file ################################################################ # Import your functions from geometry import distance, slope, intercept, line_equation def print_point(x, y): print("(", x, ",", y, ")", sep="", end="") def do_distance(x1, y1, x2, y2): print(end="The distance between ") print_point(x1, y1) print(end=" and ") print_point(x2, y2) print("is ", distance(x1, y1, x2, y2)) def do_slope(x1, y1, x2, y2): print(end="The slope of the line between ") print_point(x1, y1) print(end=" and ") print_point(x2, y2) print(end=" is ") m = slope(x1, y1, x2, y2) if m == None: print("undefined") else: print(m) def do_intercept(x1, y1, x2, y2): if slope(x1, y1, x2, y2) == None: print(end="The x-") else: print(end="The y-") print(end="intercept of the line between ") print_point(x1, y1) print(end=" and ") print_point(x2, y2) print(" is", intercept(x1, y1, x2, y2)) def do_equation(x1, y1, x2, y2): print(end="The equation of the line between ") print_point(x1, y1) print(end=" and ") print_point(x2, y2); print(end=" is ") line_equation(slope(x1, y1, x2, y2), intercept(x1, y1, x2, y2)) print() def main(): while True: # Infinite loop, use Control-C to quit p_x1, p_y1, p_x2, p_y2 \ = eval(input("Enter the point coordinates x1, y1, x2, y2 (Control-C quits): ")) do_distance(p_x1, p_y1, p_x2, p_y2) do_slope(p_x1, p_y1, p_x2, p_y2) do_intercept(p_x1, p_y1, p_x2, p_y2) do_equation(p_x1, p_y1, p_x2, p_y2) print("-----------------") main() # Run main

4. Your Code

   Create a Python source file in the same folder (or directory) as geotest.py. You must name the file geometry.py. You may use the following code as a starting point.

   # File geometry.py ############################################################ # # Modify the following functions # ############################################################ def distance(x1, y1, x2, y2): return 0.0 # Change this to return the correct value def slope(x1, y1, x2, y2): return None # Change this to return the correct value def intercept(x1, y1, x2, y2): return 0.0 # Change this to return the correct value def line_equation(m, b): print("LINE EQUATION") # Change to print the line equation

   Your task is to complete the functions in geometry.py. Do not touch any of the code in geotest.py. Unlike all the previous programming assignments, the code you write is not in control. The code provided for you is in control, and your code must be able to react to it appropriately.

5. Strategy

   To keep things simpler to begin with, don't worry about handling vertical lines and don't worry about "pretty" equation output. After everything works under those limited conditions, then implement vertical line capability and afterwards pretty output.

6. Check out

   Your finished program will be evaluated for correctness and compliance. When approved, you should submit your geometry.py Python source file to http://eclass.e.southern.edu. Be sure your name and your partner's name are included in comments at the top of each source file.