---

In this lab you will add an additional function to your geometry module, and further debug if necessary your geometry functions by testing them in a graphical application.

---

1. Teams

   You are encouraged to work with a partner for this lab. You and your partner should begin thinking about the problems and begin writing the code before lab time.

2. What to do

   You will expand the geometry module so it contains the following functions:

   • distance (same as before)
   • slope (same as before)
   • intercept (same as before)
   • line_equation_mb (makes a string representation of a line corresponding to a floating-point slope and intercept; similar to line_equation from before)
   • intersection (new function, see below)

   Your attention will be devoted exclusively to implementating the code within the file geometry.py. Download this new geometry.py file and copy the implementations of your distance, slope, and intercept functions from your previous geometry.py module. You will need to adapt your line equation function to meet some new requirements. Note that two of the functions deal with making a string instead of printing to the console. You should not touch the lineequation and point_intersection functions; they exist simply to call your functions with the expected parameters.

3. visual_geometry.py and point.py

   Add the files visual_geometry.py and point.py to the same directory as the new geometry.py file. These files contain all the necessary code to manage the graphics display. You should not modify the contents of visual_geometry.py and point.py.

4. Making a string instead of printing to the console

   The graphics code in visual_geometry.py requires a string object to render the line equations. You must provide the missing code in line_equation_mb to make a string instead of printing to the console as you did before. The skeleton code is in place in the new geometry.py file.

5. Implement a new function

   You need to implement a new function, intersection, that expects four floating-point parameters. The first parameter represents the slope of the first line (None, if the first line is vertical), the second parameter is the y-intercept of the first line (x-intercept if the line is vertical). The third and fourth parameters represent the slope and intercept of a second line:

   def intersection(m1, b1, m2, b2): # Details omitted

   The function should return a point object representing the x and y components of the point of intersection of line #1 (slope = m1, intercept = b1) and line #2 (slope = m2, intercept = b2). (Do not forget that vertical lines will have a slope of None and their intercept will be their x-intercepts.)

   The function should return None if the lines do not have a single point of intersection. The client code can then check for a valid intersection point.

   How do you compute the point of intersection of two lines?

   • If the two lines have the same slope, there is no single point of intersection. The function returns None in that case.
   • If neither line is horizontal or vertical, we have a pair of equations that look like y = m₁x + b₁
     y = m₂x + b₂ since both righthand expressions equal y, set them equal to each other: m₁x + b₁ = m₂x + b₂ and solve for x:

     m1x - m2x + b1	=	m2x - m2x + b2
     m1x - m2x + b1	=	b2
     m1x - m2x + b1 - b1	=	b2 - b1
     m1x - m2x	=	b2 - b1
     (m1 - m2)x	=	b2 - b1
     x	=	(b2 - b1)/ (m1 - m2)

     This final equation

     x = (b₂ - b₁)/ (m₁ - m₂)

     serves as a formula to compute x. Once you have x you can plug it into either of the original equations to compute y. This (x,y) point is the point of intersection of the two lines.

   • If one of the lines is vertical, you cannot use the above formula. Attempting to perform arithmetic with None will produce a runtime exception. Since you know the x-intercept of the vertical line, you can deduce the x coordinate of the intersection directly from the vertical line's intercept. You can plug this x value into the equation for the non-vertical line to compute the intersection point's y coordinate.

6. Additional remarks

   You may have to fix errors in your existing functions if the new graphical client code reveals logic errors that were not uncovered by earlier tests.

   The most common problem is an incorrect and/or incomplete intersection function. The code within visual_geometry.py depends on a correctly written intersection function to draw a line from one side of the window to the other. Since it is easy to experiment with all kinds of lines visually, your testing may reveal errors in your existing code. If you do not see any lines or lines are missing in certain situations, focus on correcting your intersection function. Pay particular attention to how you handle vertical lines.

7. Program execution

   The graphical application allows the user to interactively supply points for lines that potentially intersect.

   

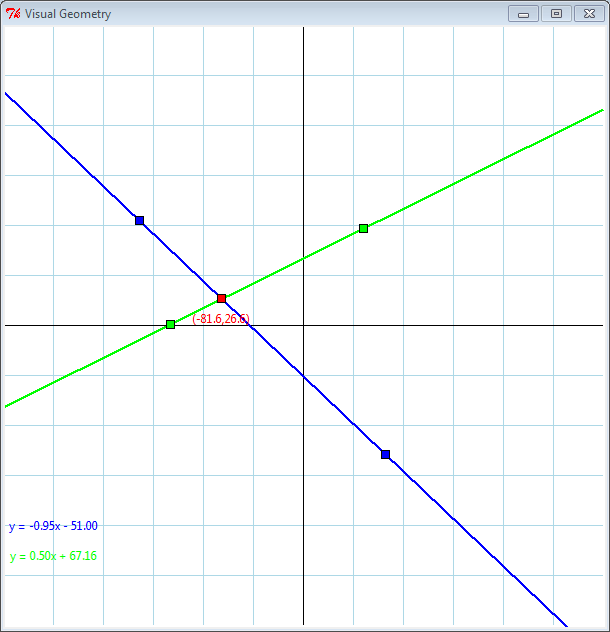
   The axes range from -300 to +300, so each square on the graph paper is 50 units wide by 50 units high.

   Some useful interface shortcuts include:

   • If you wish wish to make a vertical line immediately, click the mouse to make the initial point of the line and then press the V key to automatically generate the other point to make a vertical line.

   • If you wish wish to make a horizontal line immediately, click the mouse to make the initial point of the line and then press the H key to automatically generate the other point to make a horizontal line.

   • If you wish wish to clear all the points from the graph and make two new lines, press the Z key.

   Remember, the only file you are supposed to touch is geometry.py; do not modify the other files.

8. Check out

   Your finished program will be evaluated for correctness and compliance. When approved, you should submit your geometry.py Python source file to http://eclass.e.southern.edu. Be sure your name and your partner's name are included in comments at the top of each source file.