CPTR 124 Fundamentals of Programming
In this lab you will write a module containing multiple functions that dabble in analytic geometry.
- Teams
You are encouraged to work with a partner for this lab. You and your partner should begin thinking about the problems and begin writing the code before lab time.
- What to do
In this assignment you will manage two Python source files:
-
geometry.py. You will implement four of the functions specified in this file. We will defer one of the functions until the next assignment. More information about these functions appears below. This file constitutes thegeometrymodule. -
testgeom.py. This program uses yourgeometrymodule, allowing a user to enter in the coordinates of two geometric points. The program then prints four things:- the distance between the two points,
- the slope of the line that passes through the two points,
- the y-intercept of the line that passes through the two points, unless the line is vertical; in which case the program prints the x-intercept of the line, and
- the equation of the line (in slope-intercept form) that passes through the two points.
You should not modify this program.
geometryPython module consisting of four functions that the other file will use. The program found intestgeom.pywill not work properly until you correctly implement the expected functions.The required functions are:
- distance
The distance between two points (x1, y1) and (x2, y2), is given in the following formula:

Write a function named
distancethat accepts four floating-point arguments x1, y1, x2, and y2, in that order, representing two geometric points (x1, y1), and (x2, y2). It should return the floating-point value representing the distance between the two points. You can compute the square root of a numeric value via thesqrtfunction in the standardmathmodule. - slope
The slope of the line passing through two points (x1, y1) and (x2, y2), is the difference of the y values divided by the difference of the x values:
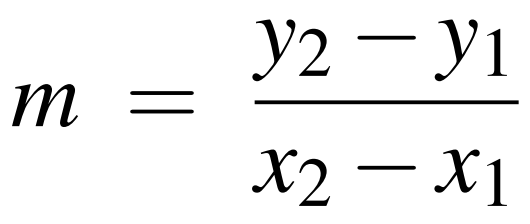
Write a function named
slopethat accepts four floating-point arguments and returns the floating-point value representing the slope of the line passing through the two points represented by the arguments.Watch out for vertical lines! Return the value
infto represent infinity if the line is vertical. Theinfvalue is defined in the standardmathmodule.Note: The function's behavior is undefined for parameters that represent two equal points. When we say the function's behavior is undefined, we mean you do not need to worry about what your function does if the client attempts to compute the slope with two points that are the same. (Later in this course we will consider how to properly handle such exceptional situations.)
- intercept
An intercept is a number that represents a location on an axis where a line intersects that axis. The y-intercept of a line is the y value of the point where a line crosses the y-axis. Write a function named
interceptthat accepts four floating-point arguments representing the coordinates of two points. The function ordinarily returns the floating-point value representing the y-intercept of the line that that passes through the two points defined by the arguments.For non-vertical lines, we can compute the y-intercept from the y = mx + b form of a line. Solving for b, we get b = y - mx:
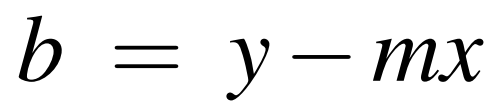
This means if we know the slope, m, we can plug in the (x, y) coordinates from either point to compute b.
Vertical lines do not have a y-intercept, so the
interceptfunction instead should return the x-intercept for vertical lines. If the two points form a vertical line, it is easy to determine the x-intercept.Note: The function's behavior is undefined for parameters that represent two equal points. Again, this means you need not worry about this possibility in your function.
- intersection
You do not need to implement this function at this time. You will implement it for the next assignment.
- lineequation
The equation of a line in slope-intercept form is
y = mx + b where m is the line's slope, and b is the line's y intercept.Write a function named
lineequationthat accepts four floating-point arguments representing coordinates of two points. It should return a text string expressing the equation of that line in slope-intercept form.A vertical line has an equation of the form
x = b
where b is the x-intercept. Your function should produce the equation for vertical lines correctly.
When creating the string round all displayed numbers to two decimal places. The equation your function produces should be "pretty," meaning do not return an equation like
y = -1.0x + -3.0rather the function should return the stringy = -x - 3.0and an equation likey = 20.5x + 0.0should appear asy = 20.5xPlace spaces around the equals symbol and the addition and subtraction symbols so the equation appears as you might see it in a mathematics textbook. This means you will need some conditional statements within yourlineequationfunction to fine tune the exact representation.It is important to note that in your
lineequationfunction you are not printing anything; instead, you are building a string that code withintestgeom.pywill print. Start with the empty string ("") and concatenate the string"y = "or"x = "depending on whether the line is vertical or not. Then concatenate the appropriate slope and intercept values as appropriate. Recall that you cannot concatenate a string and a number directly. Ifeqnis the equation string you are building andmis a variable bound to the floating-point value 2.0, to build the string"y = 2.0x"you would need to writeeqn = "y = " + str(m)in Python.As you begin developing your
lineequationfunction do not worry about pretty formatting. First concentrate on getting the numbers correct, and after you are sure the results are mathematically sound then, if you have time, proceed to make the representation more attractive.If you do not have the time or interest to make the string "pretty," you may elect to receive 9/10 points for the assignment if your string is just mathematically correct.
- floatequals
I have provided the
floatequalsfunction for you to use as needed. Remember that many floating-point numbers do not have an exact representation. This means the==operator may consider two floating-point numbers unequal even though we believe they should be equal. The graphical user interface functions are limited to the pixel size based on the screen resolution. Thefloatequalsfunction can help adjust for the graphical environment's limitations.
-
- Organization
Copy the files
geometry.pyandtestgeom.pyto the same folder (or directory). Do not change the names of the files.Your task is to complete the functions (except for
intersection) ingeometry.py. Do not touch any of the code intestgeom.py.Unlike all the previous programming assignments, the code you write is not in control. The code provided for you is in control, and your code must be able to react to it appropriately.
It is important that you not include any
printorinputstatements within your functions. The code withintestgeom.pyis responsible for obtaining input from the user and displaying the results. Also, yourdistance,slope, andinterceptfunctions should perform no rounding. Callers can round the results you compute as they see fit. It is appropriate to round the floating-point values that you use to build the line equation string in yourlineequationfunction—round these to two decimal places. - Strategy
First download the two Python source files. Before you touch the code in
geometry.pymake sure that thetestgeom.pyprogram executes without any run-time exceptions. Since you have yet to add your code to thegeometrymodule, the program will not work correctly, but it should not crash. The filegeometry.pycontains five function stubs. They each return some default value that clients are able to use without crashing.To keep things simpler to begin with, don't worry about handling vertical lines and don't worry about "pretty" equation output. Make sure your code works properly with
testgeom.pywith simple, limited examples. After everything works under those restricted conditions, then implement vertical line capability and afterwards pretty output.Note that to execute your program within the Wing IDE the
testgeom.pyeditor window must be the active editor window. If you attempt to run the program with thegeometry.pyfile active, the program will not run. So, edit (but do not run) thegeometry.pyfile, and run (but do not edit) thetestgeom.pyfile. - Check out
Double check to make sure your
distance,slope, andinterceptfunctions are returning numbers, not strings and that they are doing no rounding. Yourlineequationfunction should return a string.Your finished module will be evaluated for correctness and compliance. When approved, you should submit your
geometry.pyPython source file to http://eclass.e.southern.edu. Be sure your name and your partner's name are included in comments in the first line of your source file.